A linear layer takes a set of inputs, and for each node in its layer it sums weights*inputs to calculate the node output. This output is then fed to the next layer (or is the network output if it's the final layer).

Neural network architectures are often static, what you define before training is the final architecture for the network. If your network is too small to model the dataset, it's often thrown away and a new network created with new random values.

How can we avoid re-learning what was already learned if we want to add nodes to our network?

Defining our goals

1. Don't increase the loss at expansion time.
2. Start from a state that can be learned from.
3. Add addition nodes to the layer.

Possible uses

1. Expand multiple times throughout training, to hopefully reduce overall training compute required (unconfirmed).
2. Re-use an existing model with expanded

Implementation

To expand the linear layer, we need new weights for calculating the node, as well as new weights for the next layer to use the nodes output.

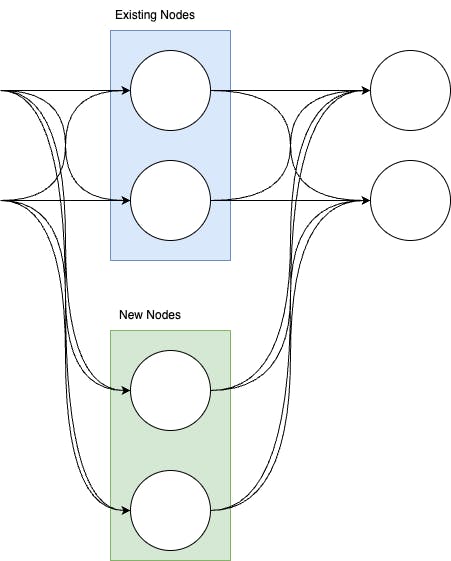
The code for this would look something like

      self.linear2.weight = torch.nn.Parameter(torch.cat((self.linear2.weight, torch.zeros(self.output_dims, new_node_count)), dim=1))

      self.linear.weight = torch.nn.Parameter(torch.cat((self.linear.weight, torch.rand(new_node_count, 2)), dim=0))
      self.linear.bias = torch.nn.Parameter(torch.cat((self.linear.bias, torch.zeros(new_node_count))))

A fully working minimal example of this can be found here.

Let's review this against our goals.

Same loss as the previous network

With a weight of zero as above, all contribution of the new nodes to the loss would be exactly zero.

State that can be learned from

The core of most deep learning is gradient descent. This works by following the gradients of our loss function for each weight in our network, thus minimizing loss.

The question then is whether our new nodes have a gradient for our newly added weights of zero.

The gradient of a layer can be viewed as the following, where w_next is the weights to the next layer, d_next is the error from the next layer, and output_current is the output of the layer in question.

grad = w_next * d_next * output_current

With the above, I'd answer yes.

Pitfalls

1. Setting linear layer output weights and input weights to all zeros.
   1. This leads to the derivative of all the new weights added to always be zero.
2. Setting a linear layer weight (output or input) to zeros and the other to a specific value (not random).
   1. This would result in all expanded nodes having the same values with no way to escape.
3. Copying an existing node and halving its output weights.
   1. In this case the node would be "collapsed" causing the 2 nodes to always have the same value. This doesn't help with learning, but increases compute. I'd expect perturbing the values some small amount to still run into this given enough time while still increasing loss at expansion time.