ML Experiment Log - NN + Polynomial Solvers Pt. 2
In the previous attempt, a polynomial based neural network was setup and we had some inconsistent results coming back.
My assumption at that point was that the correct solutions weren't being found, and maybe the work of the solver needed simplified.
Reducing scope the solver needs to deal with
To simplify, I wanted to explore the possibility of running the polynomial solvers on only a specific layer at a time. This entails a few of the following changes. I choose the hidden layer as the part to train.
- Save a random value for all variables not part of the layer that's training.
- Substitute the random values in their places in loss, output, etc functions.
- Run solve for only the variables part of the layer being trained.
Results
After making these changes, results return very quickly, however using reversing the order of variables passed to the solve call is still resulting in no solutions being returned.
The results though still had a fairly high loss, and didn't seem to be producing good output. I thought this probably meant the architecture wasn't complex enough to represent the problem (despite some quick google suggesting it was). The following is the architecture that was used at that point (no bias, no activations used).
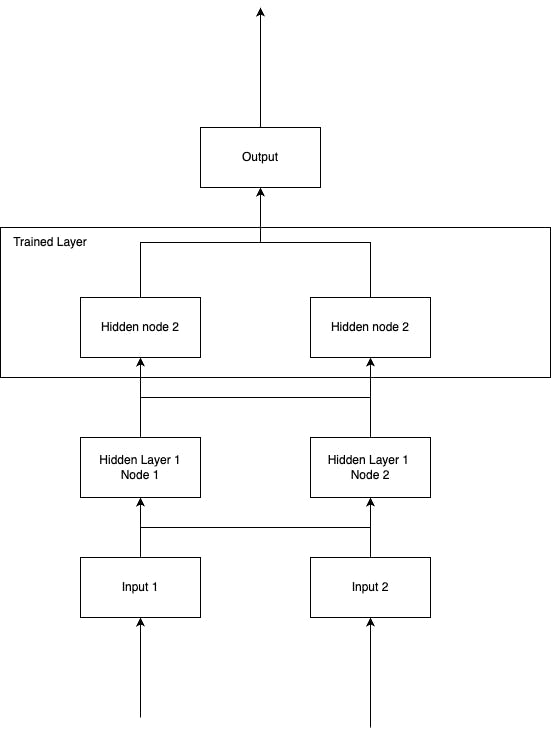
Iterating
With the above results suggesting architecture may not be complex enough, I thought probably what was missing was some form of non-linearity. This is typically an activation function.
It's possible to represent sigmoid as an activation function but it would likely get a bit complex as it would require many terms to have a good approximation. Relu isn't easy represented by polynomials accurately.
I decided to try multiplying the nodes from each layer by each other to be a 3rd node coming from each layer.
Multiplying nodes for non-linearity
Multiplying nodes together was causing the solver to take significantly longer to find solutions. I suspect 2 reasons: increased number of weights per node, higher degree polynomials making solving harder.
As a result I reduced the weight we're solving for down to a single weight per polynomial solve, with surprising results.
The following is what that architecture looks like.
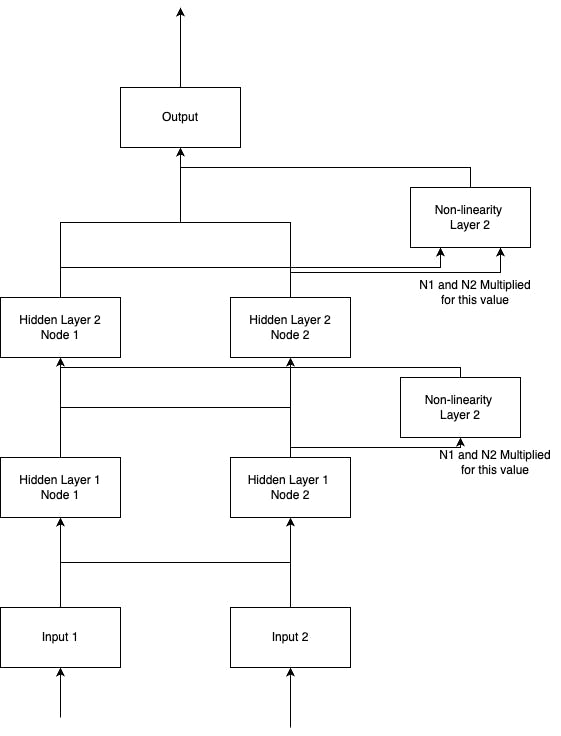
Results
Results return quite quickly, and actually fully solve it (generally less than 1e-10 error). This is surprising to me since we're only actually training one node, and the rest of the network is fully random.
Potential next steps
- Try on a larger problem (especially with a larger dataset), maybe mnist.
- Make variable training more dynamic to allow looping through all variables in the network.
